Written by Allen Wyatt (last updated January 31, 2022)
This tip applies to Excel 2007, 2010, 2013, and 2016
Neil knows how to calculate a simple internal rate of return using the IRR function. He wonders, though, how to calculate an IRR on a more complex deal, such as monthly repayments on a 36-month term where the first 12 months are interest free and the next 24 months are at 5% interest.
It is helpful to understand what is meant by the internal rate of return (IRR). This is, itself, an interest rate (the return) averaged over the life of the loan. Thus, the interest rate being charged on the loan doesn't really come into play. (This is evidenced by the fact that the parameters for Excel's IRR function don't include an interest rate parameter.) The only thing that matters is the principal, the term, and when repayments are made.
Since Neil is receiving regular monthly repayments, then the IRR function is, indeed, the one to use. Excel includes variations on the IRR function, as well, but they are probably not appropriate. The MIRR function calculates the IRR when you reinvest the repayments. It allows you to specify an interest rate, but this rate is applied to the reinvestment of the repayments; it is not the interest rate you charge to the person repaying you.
The other IRR-related Excel function is the XIRR function. This isn't appropriate for Neil's needs because it is used to calculate the IRR when the repayments are not regular. For example, you may only get repayments on certain months of the year. Since Neil is receiving regular monthly payments, the IRR function is still the best to use.
Let's look at how this would work in Neil's case, then. Let's say that he gives a loan of $50,000 to someone at 5% interest. This interest is only applicable for the last 24 months of the loan, as Neil indicates that the first 12 months are interest free. Thus, payments for the first 12 months would be $1,388.89 per month, which is calculated by simply dividing $50,000 by 36.
After that first year, payments would be $1,462.38 because the person is essentially getting a $33,333.32 loan (the remaining balance, which is 2/3 of the original loan amount) at 5% interest for 24 months.
When calculating the IRR, you have, then, 36 calculated payments—12 of them at $1,388.89 and then 24 of them at $1,462.38. Place the original value into cell A1 (as a negative value) and the payments (as positive values) into cells A2:A37. You can then apply the IRR function to the range of 37 values. (See Figure 1.)
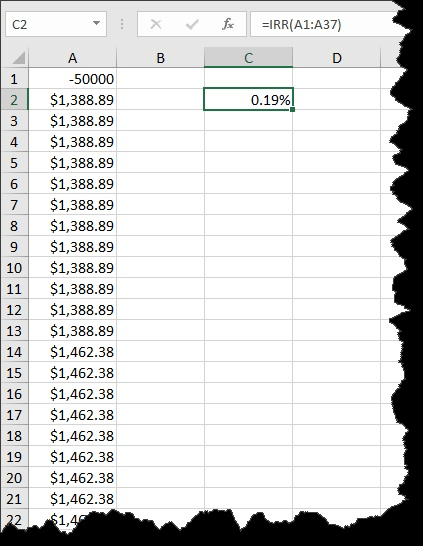
Figure 1. Calculating the IRR based on a $50,000 loan.
Note that the IRR is 0.19%. Since the cash flows represent montly payments, this is the IRR per month. To adjust it to show as an annual rate, just multiply it by 12 and you come up with an annual IRR of 2.24%. This is what Neil is actually earning on his loan of $50,000. It is the average interest earned over the life of the loan. It turns out to be quite a bit lower than the 5% interest rate because a third of the loan term is really interest free.
It should be noted that all of these calculations are based on the note really being interest free for the first 12 months. If that is not the case—if the interest is simply deferred to be repaid during the last 24 months—then the result is quite different, but the calculations are the same. The person repaying the loan would still only pay $1,388.89 per month for the first 12 months. However, since interest is still be calculated, after the first year the outstanding balance is $35,504.12.
This outstanding balance is then used to determine the regular payment for the remaining 24 months, which would be a monthly payment of $1,557.62. Plugging those figures into the same repayment schedule calculates a new IRR of 0.42%, annualized to exactly 5%. (See Figure 2.)
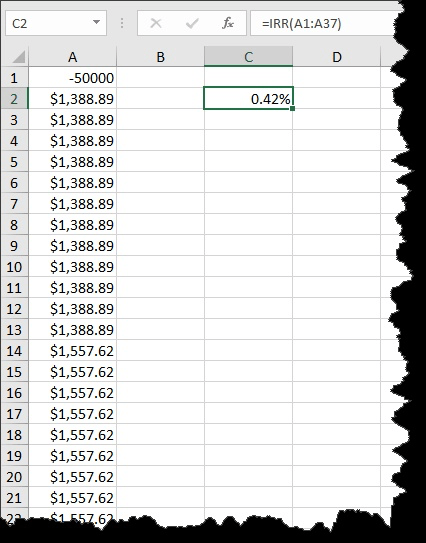
Figure 2. Calculating the IRR based on a $50,000 loan, with deferred interest.
ExcelTips is your source for cost-effective Microsoft Excel training. This tip (4359) applies to Microsoft Excel 2007, 2010, 2013, and 2016.
Create Custom Apps with VBA! Discover how to extend the capabilities of Office 2013 (Word, Excel, PowerPoint, Outlook, and Access) with VBA programming, using it for writing macros, automating Office applications, and creating custom applications. Check out Mastering VBA for Office 2013 today!
There are times when it can be beneficial to combine both numbers and text in the same cell. This can be easily done ...
Discover MoreHate to take your hands off the keyboard while working on a worksheet? Here's one way to activate the Formula Bar without ...
Discover MoreOne of the staples of high school algebra classes is the quadratic equation. If you need to solve such equations in ...
Discover MoreFREE SERVICE: Get tips like this every week in ExcelTips, a free productivity newsletter. Enter your address and click "Subscribe."
2018-10-31 11:50:57
Willy Vanhaelen
@Rajesh
With irregular interest & principal repayments you have to use the XIRR function.
2018-10-30 04:49:49
Rajesh
How would I calculate the interest rate for a loan given for 6 years with irregular interest & principal repayments ??
2017-09-09 13:18:16
Terence F. Cuff
I dissent from the view that the XIRR function is not appropriate in this situation. You state: "The other IRR-related Excel function is the XIRR function. This isn't appropriate for Neil's needs because it is used to calculate the IRR when the repayments are not regular. For example, you may only get repayments on certain months of the year. Since Neil is receiving regular monthly payments, the IRR function is still the best to use."
I am not overly fond of the IRR function on account of its lack of economic precision and identified flaws in the function where it occasionally will produce mathematically inaccurate results. The IRR function can be dangerously biased in appropriate circumstances, since it does not pay attention to the precise day on which cash flows are paid or received. This usually is not a problem for monthly payments that are not large amounts; this can make a considerable difference when IRR is used with a quarterly, semi-annual, or annual convention and payments are large. (This also can invite economic manipulation.) For example, it makes a big difference whether a $1 million payment is made on January 1 or December 31. The IRR function does not distinguish between the two; if you are using an annual convention, all cash flows during the year are bundled together. The XIRR function does distinguish, and it can make a big difference. Nevertheless, the IRR function often provides "good enough" approximations of internal rate of return for purposes in most situations.
Also, as Microsoft readily admits, both IRR and XIRR use a limited number of iterations and may not find an internal rate of return solution when one exists. Further, there can be multiple solutions to internal rate of return. The IRR and XIRR functions, without special coaxing, will find only one solution. These two functions may find a solution to internal rate of return that really is not appropriate for your current uses.
Setting these issues aside, a loan rarely is repaid with equal payments over equal periods, which your comments assume. Different months have different numbers of days. There is a different number of days in each payment period. You may choose to ignore that, but whatever you may want to imagine, different months have different numbers of days, and that should make a difference in computing internal rate of return. Also, payments may not be made on the last day of the month. XIRR treats all payments as made on the last day of the month unless you choose the first day of the month convention. The XIRR function provides greater texture and precision to determining the internal rate of return than the IRR function, which assumes that all months have the same number of days and that all payments are made on the last day of the month.
Additionally, the XIRR function in effect offers a blending function to take account the differences between years that have 365 and 366 days. This is a view of internal rate of return that may or may not be appropriate. Some people computing internal rate of return will reject even the XIRR function as not being precisely correct, depending on how you want to define internal rate of return. I find that few applications demand this level of precision. Depending on how you want to define internal rate of return and how much precision you need, you may have to define your own internal rate of return function and then to solve it iteratively.
I find that it often is appropriate to use the IRR function with monthly cash flows for purposes of financial and tax projections. I almost always recommend that attorneys use the XIRR function for computations that will have a legal effect (if they have to define legal relationships using Excel), such as economic terms in a promissory note that depend on internal rate of return. I will avoid both the IRR and XIRR functions if I am defining legal relationships and much is at stake. I define the relationships by formula. I then will set up an iterative procedure to find the solution and not rely on IRR or XIRR.
You may say that the difference between the number computed using the XIRR and the IRR functions may differ little. That often is the case. Sometimes the difference is dramatic.
Got a version of Excel that uses the ribbon interface (Excel 2007 or later)? This site is for you! If you use an earlier version of Excel, visit our ExcelTips site focusing on the menu interface.
FREE SERVICE: Get tips like this every week in ExcelTips, a free productivity newsletter. Enter your address and click "Subscribe."
Copyright © 2024 Sharon Parq Associates, Inc.
Comments