Please Note: This article is written for users of the following Microsoft Excel versions: 2007 and 2010. If you are using an earlier version (Excel 2003 or earlier), this tip may not work for you. For a version of this tip written specifically for earlier versions of Excel, click here: Converting From Numbers to Text.
Jocelyn asked if there is a way to easily convert numbers to their text equivalent. For instance, to convert the numeric value 6789 to the text digits "6789."
There are multiple ways that you can approach this problem. One way is to simply specify to Excel that the cells should be treated as text. Display the Format Cells dialog box and then on the Number tab make sure that Text is selected. Any selected cells are then formatted as if they were text, and are moved to the left side of their cells (unless you have some other alignment format specified).
The applicability of this solution, however, depends on the version of Excel you are using. In some versions it will work as described here, but in others it may not. There is another thing you can try, however:
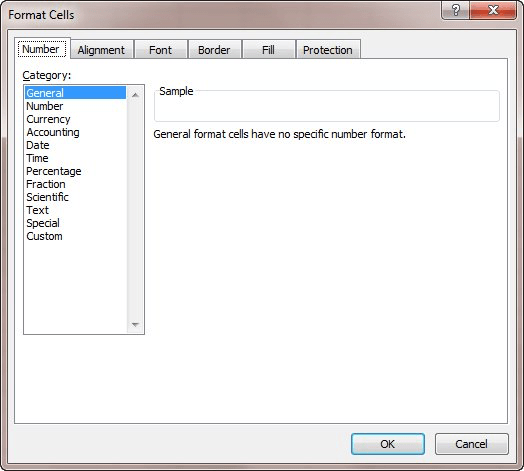
Figure 1. The Number tab of the Format Cells dialog box.
Another thing you can do is to use the TEXT worksheet function. Let's say you have the value 6789 in cell A7. In cell B7 you could place the following:
=TEXT(A1, "#,##0.00")
This usage of TEXT results in a text digits that have the thousands separator in the right place and two digits to the right of the decimal point, as in "6,789.00". You can specify, as the second parameter to TEXT, any formatting desired. If you want the number converted to text without any special formatting, you can use the following:
=TEXT(A1, "0")
The result is the textual equivalent of an integer value.
ExcelTips is your source for cost-effective Microsoft Excel training. This tip (6230) applies to Microsoft Excel 2007 and 2010. You can find a version of this tip for the older menu interface of Excel here: Converting From Numbers to Text.

Dive Deep into Macros! Make Excel do things you thought were impossible, discover techniques you won't find anywhere else, and create powerful automated reports. Bill Jelen and Tracy Syrstad help you instantly visualize information to make it actionable. You’ll find step-by-step instructions, real-world case studies, and 50 workbooks packed with examples and solutions. Check out Microsoft Excel 2019 VBA and Macros today!
Want a quick way to replace background colors in cells? It's easy to do using Find and Replace, or you can simply use the ...
Discover MoreBy default, Excel vertically aligns cell contents to the bottom of cells. If you prefer a different default alignment, ...
Discover MoreNeed to cram a bunch of text all on a single line in a cell? You can do it with one of the lesser-known settings in Excel.
Discover MoreFREE SERVICE: Get tips like this every week in ExcelTips, a free productivity newsletter. Enter your address and click "Subscribe."
2020-10-23 16:15:53
Roy
General thought is that if the need involves a downstream use of the cell value, one can place the TEXT() formula, or the Joining (@Arnstein) in that place leaving real numbers in the original data cells. You know, "if"...
@Rajnikant Padole: The current version of O365 offers a Translate option on the context menu. It is not formula addressable, so each use is a physical action, but it can be done inside Excel so no need to use, perhaps, Google Translate. The output is copyable so also pastable but it simply won't let you use it non-interactively. Although, it is possible VBA offers the option of either addressing this functionality via VBA or addressing the basic idea via any available translator, browser based or dedicated app. If so, a UDF would be possible, one thinks.
Side note: a separate thought, which could be used here, is the VBA Immediate Window. Consider that it will let you run working VBA a line at a time. One can have his macro cake and eat it too! First, consider it for many small tasks. Open it, run the single line that does the single need, and done. A fantastic use I saw mentioned recently was by the My Online Training Hub people (low impact and useful, like this site) to add a formula to, oh, 100,000 cells at once. For a large number of tasks, one could figure the appropriate VBA command, or ask for help with that, record it somewhere in the spreadsheet, and copy and paste when needed. That'd be the simplest use, single shot things, stored in the workbook they were written in. Second, one could expand on that to have a dedicated workbook with these one-liners neatly organized, however makes sense to the user, and open it first, then have it available as desired during normal work. Third, the IW can only run a single line, but many VBA commands I've seen over the years seem combinable, as people do precisely that in their actual macros, if only to claim the macros are fewer lines. It's not necessary to do that and normal programming practice I'm sure frowns upon it as "opaque" (yeah, no doubt!), but people do it so... one might be able to do any given task in a one-liner that way. Or not. Leading to... Fourth, well, one line at a time, but there's no rule to keep you from then running another single line, then another and so on... Lots of copy and paste, but notice, you still get the power functionality of a macro, which can be mind-bendingly simple compared to the contortions of doing quite a few things in formulas, WITHOUT having to save the spreadsheet as a macro-enabled spreadsheet. Downsides, it has a few, but then again too few to... no, one can mention them: well, any other user might balk a bit at it as it would be a foreign way of working at present, though if it caught on, it might seem nifty... not there yet though. And several steps are several steps where many people regard one step as just beastly. No declaring variables either, or interacting with it directly. So... not a slamdunk, not perfect. But fifth, I wonder, and do not know the answer — which, if it would work nicely, would let you do normal macros this way too — if one could maintain a simple "calling" macro that could be pasted into the spreadsheet as a real macro that saving it later would each time as an XLSX strip off, that could take a series of one-liners, or a real, full macro written and tested, then the text of it copied out like the one-liners, and run them. So the macro you paste in each time would be cookie cutter, just edit to give it the range with the commands it needs, then work along and when needed, run it, perhaps even give it a dialog to ask for the set to run so it works without "editing" editing, giving you real macros, or at least ease in performing more than one one-liner in a row, while still always being stripped off when saving.
How's that apply here? Well, use the BAHT() formula, then run a one-liner, or several if needed, to access some translator and deposit the translation where needed.
In general though guys, these conversions all have one weakness. I wrote one 25 years ago in Excel 97, formulas, not a macro, that I used for four years and was wonderfully happy with. Then never needed it again. But it would be a constant source of pain for everyone else because everyone else would want some small to major change or six (I've been reading these requests for 10 years now). One guys want something saying "one thousands..." while another abhors that "s" computers tack onto single items. Another wants proper case while another wants every word's first letter capitalized while another wants every number word capitalized, fully, but the filler words just first letter. Another wants Portuguese ('cuase, you know, he's Portuguese) and another wants the Indian conventions. Another wants "and twenty-three cents" (yes, for gosh sake) while someone else wants "and 23/100" and another "and 23/100ths" and so on, sometimes as personal choice, sometimes to match a paper check he has to print on. And others need other uses, perhaps in contracts or other legal documents, commercial invoices for at least two different governments to make use of with their own requirements, and worse, preferences. Then you have the people requiring space-fillers, asterisks leading and lagging perhaps, even X-number of "$" characters to fill in before the numbers (so "$$$$$$$$$$$$435.75**" (an example from yesterday for me... helpful tip: the bank's software couldn't figure that out, so...).
My wager is that's why we don't see a question like this answered everywhere with a quck "go to this (fill in the blank with any of three website, say) website and they have a fantastic one. Any time folks finally want to work on standardizing the idea, I bet that path becomes enabled and we're all happy.
But even one work bit is sooooo beastly...
2017-03-07 06:38:55
Arnstein
Number to TEXT
=A1&""
2017-03-07 04:56:38
Ken Varley
Typo......
Formula refers to cell A1
Explaination refers to cell A7
2016-06-25 03:44:01
Anand Mundada
In the Cell A1 has value of 5, i want to convert in to text i.e. pass, if value is 3 ATKT and if value is 4 Fail in same cell or in another cell. How it can be done
2016-06-25 01:14:51
Dear sir,
How can l convert number to text. E.g 1500 in cell C1 and the result in C4 should "one thousands five hundred only"
2016-05-08 19:16:05
Gil Fabia
How can I put into a cell the number of times i opened the worksheet or an excel file? Everytime i open a file 1 is added to to a specific cell say A1. Cell A1 will be showing 20 if the file is opened at the 20th times. If i open it on the 21st time then, A1 will be 22. Thank you and more power.
2015-12-29 09:12:53
Rajnikant Padole
1234
Formula
=BAHTTEXT(A2)
Displays the number in text. (One thousand two hundred thirty four Baht in Thai text)
result - หนึ่งพันสà¸à¸‡à¸£à¹‰à¸à¸¢à¸ªà¸²à¸¡à¸ªà¸´à¸šà¸ªà¸µà¹ˆà¸šà¸²à¸—ถ้วน
please text show in u.s. english
2015-09-04 07:31:32
Well, to get text from a number (ex: 56 return fifty six) i use this function.
But i am portuguese, so it works for portuguese numbers.
I have no time to explain more, but could be important, and you can adapt.
Further more, the funtion works, but i have intention to improve the function (when i have the time).
syntax to use in portuguese:
=extenso(nº, type)
nº= number.
Range: 0 to 999999999.99
Two decimals (max)
type= -1 or 0 or 1 or 2
-1 = none
0 = text for units: number
1 = text for units: Euros
2 = text for units: Reais (UM Brasil)
>2 = 0
Function
************
Function extenso(nValor As String, nPNR_Tipo As Integer) As String
If IsNull(nValor) Or nValor > 999999999.99 Then Exit Function
Dim PNR_Tipo As Integer
Dim PNR_Unid_Plural As String
Dim PNR_Unid_Singular As String
Dim PNR_Cent_Plural As String
Dim PNR_Cent_Singular As String
If nPNR_Tipo > 2 Then
nPNR_Tipo = 0
End If
PNR_Tipo = nPNR_Tipo
If PNR_Tipo = 0 Then
PNR_Unid_Plural = "unidades "
PNR_Unid_Singular = "unidade "
PNR_Cent_Plural = "centésimas"
PNR_Cent_Singular = "centésima"
End If
If PNR_Tipo = 1 Then
PNR_Unid_Plural = "Euros "
PNR_Unid_Singular = "Euro "
PNR_Cent_Plural = "Cêntimos"
PNR_Cent_Singular = "Cêntimo"
End If
If PNR_Tipo = 2 Then
PNR_Unid_Plural = "Reais "
PNR_Unid_Singular = "Real "
PNR_Cent_Plural = "Centavos"
PNR_Cent_Singular = "Centavo"
End If
If PNR_Tipo = -1 Then
PNR_Unid_Plural = ""
PNR_Unid_Singular = ""
PNR_Cent_Plural = ""
PNR_Cent_Singular = ""
End If
'Declara as variáveis da função
Dim intContador As Integer
Dim intTamanho As Integer
Dim strValor As String
Dim strParte As String
Dim strFinal As String
Dim strGrupo(4) As String
Dim strTexto(4) As String
'Define matrizes com extensos parciais
Dim strUnid(19) As String
strUnid(1) = "um ": strUnid(2) = "dois ": strUnid(3) = "três ": _
strUnid(4) = "quatro ": strUnid(5) = "cinco ": strUnid(6) = "seis ": strUnid(7) = "sete ": _
strUnid(8) = "oito ": strUnid(9) = "nove ": strUnid(10) = "dez ": strUnid(11) = "onze ": _
strUnid(12) = "doze ": strUnid(13) = "treze ": strUnid(14) = "catorze ": _
strUnid(15) = "quinze ": strUnid(16) = "dezasseis ": strUnid(17) = "dezassete": _
strUnid(18) = "dezoito ": strUnid(19) = "dezanove "
Dim strDezena(9) As String
strDezena(1) = "dez ": strDezena(2) = "vinte ": strDezena(3) = "trinta ": _
strDezena(4) = "quarenta ": strDezena(5) = "cinquenta ": strDezena(6) = "sessenta ": _
strDezena(7) = "setenta ": strDezena(8) = "oitenta ": strDezena(9) = "noventa "
Dim strCentena(9) As String
strCentena(1) = "cento ": strCentena(2) = "duzentos ": strCentena(3) = "trezentos ": _
strCentena(4) = "quatrocentos ": strCentena(5) = "quinhentos ": strCentena(6) = "seiscentos ": _
strCentena(7) = "setecentos ": strCentena(8) = "oitocentos ": strCentena(9) = "novecentos "
'Divide o valor em vários grupos
strValor = Format$(nValor, "0000000000.00")
strGrupo(1) = Mid$(strValor, 2, 3) 'Milhão
strGrupo(2) = Mid$(strValor, 5, 3) 'Milhar
strGrupo(3) = Mid$(strValor, 8, 3) 'Centena
strGrupo(4) = "0" + Mid$(strValor, 12, 2) 'Centavo
'Processa cada grupo
For intContador = 1 To 4
strParte = strGrupo(intContador)
intTamanho = Switch(Val(strParte) < 10, 1, Val(strParte) < 100, 2, Val(strParte) < 1000, 3)
If intTamanho = 3 Then
If Right$(strParte, 2) <> "00" Then
strTexto(intContador) = strTexto(intContador) + strCentena(Left(strParte, 1)) + "e "
intTamanho = 2
Else
strTexto(intContador) = strTexto(intContador) + IIf(Left$(strParte, 1) = "1", "cem ", strCentena(Left(strParte, 1)))
End If
End If
If intTamanho = 2 Then
If Val(Right(strParte, 2)) < 20 Then
strTexto(intContador) = strTexto(intContador) + strUnid(Right(strParte, 2))
Else
strTexto(intContador) = strTexto(intContador) + strDezena(Mid(strParte, 2, 1))
If Right$(strParte, 1) <> "0" Then
strTexto(intContador) = strTexto(intContador) + "e "
intTamanho = 1
End If
End If
End If
If intTamanho = 1 Then
strTexto(intContador) = strTexto(intContador) + strUnid(Right(strParte, 1))
End If
Next intContador
'Gera o formato final do texto
If Val(strGrupo(1) + strGrupo(2) + strGrupo(3)) = 0 And Val(strGrupo(4)) <> 0 Then
strFinal = strTexto(4) + IIf(Val(strGrupo(4)) = 1, PNR_Cent_Singular, PNR_Cent_Plural)
Else
strFinal = ""
If Val(strGrupo(2)) = 0 And Val(strGrupo(3)) = 0 And Val(strGrupo(4)) = 0 Then
strFinal = strFinal + IIf(Val(strGrupo(1)) <> 0, strTexto(1) + IIf(Val(strGrupo(1)) > 1, "milhões de ", "milhão de "), "")
End If
If Val(strGrupo(2)) <> 0 And Val(strGrupo(3)) = 0 And Val(strGrupo(4)) = 0 Then
strFinal = strFinal + IIf(Val(strGrupo(1)) <> 0, strTexto(1) + IIf(Val(strGrupo(1)) > 1, "milhões e ", "milhão e "), "")
End If
If Val(strGrupo(2)) = 0 And Val(strGrupo(3)) <> 0 And Val(strGrupo(4)) = 0 Then
strFinal = strFinal + IIf(Val(strGrupo(1)) <> 0, strTexto(1) + IIf(Val(strGrupo(1)) > 1, "milhões e ", "milhão e "), "")
End If
If Val(strGrupo(2)) <> 0 And Val(strGrupo(3)) <> 0 And Val(strGrupo(4)) = 0 Then
strFinal = strFinal + IIf(Val(strGrupo(1)) <> 0, strTexto(1) + IIf(Val(strGrupo(1)) > 1, "milhões, ", "milhão, "), "")
End If
If Val(strGrupo(2)) <> 0 And Val(strGrupo(3)) <> 0 And Val(strGrupo(4)) <> 0 Then
strFinal = strFinal + IIf(Val(strGrupo(1)) <> 0, strTexto(1) + IIf(Val(strGrupo(1)) > 1, "milhões, ", "milhão, "), "")
End If
If Val(strGrupo(2)) <> 0 And Val(strGrupo(3)) = 0 And Val(strGrupo(4)) <> 0 Then
strFinal = strFinal + IIf(Val(strGrupo(1)) <> 0, strTexto(1) + IIf(Val(strGrupo(1)) > 1, "milhões, ", "milhão, "), "")
End If
If Val(strGrupo(2)) = 0 And Val(strGrupo(3)) = 0 And Val(strGrupo(4)) <> 0 Then
strFinal = strFinal + IIf(Val(strGrupo(1)) <> 0, strTexto(1) + IIf(Val(strGrupo(1)) > 1, "milhões de ", "milhão de"), "")
End If
If Val(strGrupo(2)) = 0 And Val(strGrupo(3)) <> 0 And Val(strGrupo(4)) <> 0 Then
strFinal = strFinal + IIf(Val(strGrupo(1)) <> 0, strTexto(1) + IIf(Val(strGrupo(1)) > 1, "milhões, ", "milhão, "), "")
End If
If Val(strGrupo(3)) = 0 Then
strFinal = strFinal + IIf(Val(strGrupo(2)) <> 0, strTexto(2) + "mil ", "")
Else
If Val(strGrupo(4)) = 0 Then
strFinal = strFinal + IIf(Val(strGrupo(2)) <> 0, strTexto(2) + "mil e ", "")
Else
strFinal = strFinal + IIf(Val(strGrupo(2)) <> 0, strTexto(2) + "mil, ", "")
End If
End If
If Val(strGrupo(4)) = 0 Then
strFinal = strFinal + strTexto(3) + IIf(Val(strGrupo(1) + strGrupo(2) + strGrupo(3)) = 1, PNR_Unid_Singular, PNR_Unid_Plural)
Else
strFinal = strFinal + strTexto(3) + IIf(Val(strGrupo(3)) <> 1, IIf(Val(strGrupo(1) + strGrupo(2) + strGrupo(3)) = 1, PNR_Unid_Singular, PNR_Unid_Plural), PNR_Unid_Singular)
End If
strFinal = strFinal + IIf(Val(strGrupo(4)) <> 0, "e " + strTexto(4) + IIf(Val(strGrupo(4)) = 1, PNR_Cent_Singular, PNR_Cent_Plural), "")
End If
'If Left(strFinal, 1) = "u" Then
' extenso = "H" & Mid$(strFinal, 1)
'Else
extenso = UCase(Mid$(strFinal, 1, 1)) & Mid$(strFinal, 2)
'End If
Dim aux As String
''* 150
aux = Trim(extenso)
'' e alterar esta linha para trim(extenso)
' While Len(Trim(aux)) <> 150
' aux = Trim(aux) & "-$"
' Wend
extenso = LCase(aux)
End Function
2015-09-04 03:50:08
pravin patil
1234
Formula
=BAHTTEXT(A2)
Displays the number in text. (One thousand two hundred thirty four Baht in Thai text)
result - หนึ่งพันสà¸à¸‡à¸£à¹‰à¸à¸¢à¸ªà¸²à¸¡à¸ªà¸´à¸šà¸ªà¸µà¹ˆà¸šà¸²à¸—ถ้วน
please text show in u.s. english
2015-08-01 05:47:55
Kavitha
I Want the Expanded value of numbers
for ex.
If i key 14153.23
the net result should be
Fourteen Thousand One Hundred and Fifty Three and Twenty Three
Please Help
2015-06-05 08:50:19
Liquid acer
@vicky
check this link for sample of converting nos. into words in Excel
HOPE this help
https://youtube.com/watch?v=gTQiNAk6YxE
2015-04-28 11:37:49
Glenn Case
Vicky:
Check out http://excelribbon.tips.net/T008351_Converting_Numbers_Into_Words.html
2015-04-25 10:38:40
Michael
Conceptually, you could do it in a loop, digit by digit, starting from the right, concatenating results in a leftwise direction, picking the text from a table. The single digit zero and the tens digits are special cases which complicate things a bit. Probably better done in Office C# or VBA, which, regrettably, is above my pay grade.
2015-04-24 15:25:10
Sten-Sture
I have a column with 650 rows with contents like the following 07:12 and Excel thinks it is a number, I want to convert it to a text string!
The reason is that I have some other text values in the same column, and like to sort all om the as text values.
2015-04-24 07:47:57
VICKY
I want the value of cell C2 is 1500 to be converted as 'One thousand five hundred" in cell C5
Got a version of Excel that uses the ribbon interface (Excel 2007 or later)? This site is for you! If you use an earlier version of Excel, visit our ExcelTips site focusing on the menu interface.
FREE SERVICE: Get tips like this every week in ExcelTips, a free productivity newsletter. Enter your address and click "Subscribe."
Copyright © 2026 Sharon Parq Associates, Inc.
Comments